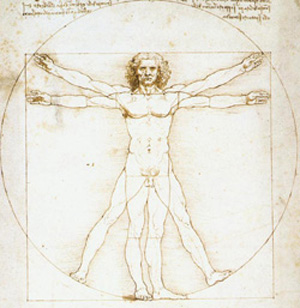
Si hay algo verdaderamente fascinante en el mundo que nos rodea es que lo podemos comprender, que es accesible a la mente Si bien los principios primeros y los fines ultérrimos se nos escapan, el universo en general está sujeto a leyes que podemos descubrir a través de la observación, la investigación y el estudio. En palabras de John D. Barrows; fïsico ingles; la razön de que hayamos tenido tanto ëxito en desvelar el funcionamiento interno del universo es que hemos descubierto el lenguaje en el que parece estar escrito el libro de la naturaleza. En el fondo no hace más que citar a Galileo Galilei, quien decía que Dios había creado el universo y había escrito sus leyes en el lenguaje de las matemáticas. El porqué esto es así en el fondo es un verdadero misterio; ¿son las matemáticas, las formas geométricas, una herramienta fabricada por nuestra mente, o más bien tienen existencia independiente y están fuera de ella? Para Roger Penrose, uno de los mejores matemáticos actuales y co-creador junto con Stephen Hawkings de la entropía de los agujeros negros, las matemáticas de alguna manera “están ahí”, y el matemático lo único que hace es descubrirlas. Es un ferviente defensor del platonismo y de la teoría de los arquetipos platónicos, imágenes o modelos primeros que existen en la mente de Dios y que utiliza al crear el universo. Así, la filosofía profunda y las matemáticas superiores caminan juntas cogidas de la mano. Desde el amanecer de la historia el ser humano ha tratado de descubrir las leyes que gobiernan el universo. Es una constante en la naturaleza humana la investigación, el buscar regularidades y patrones en el mundo que nos rodea y en nosotros mismos. Hoy en día con la teoría del Diseño Inteligente, resurge la vieja Idea de que todo en el universo responde a una Armonía Íntima, que la simple casualidad no basta para explicar desde la forma de doble espiral del ADN, hasta la íntima resonancia entre los átomos de berilio y helio, que permite que en el interior de las estrellas se catalice la reacción termonuclear de síntesis del carbono, elemento básico para el soporte de la vida. En palabras de Freeman Dyson “Cuanto más examino este universo surgido del Big Bang, y los detalles de su arquitectura, encuentro más evidencias de que, en algún sentido, el universo sabía que nosotros íbamos a llegar”. No hay mejor huella de esta armonía universal, de este diseño inteligente del universo, como postula la ciencia moderna, que la vieja idea de la Divina Proporción (según Luca Pacioli), sección áurea para Leonardo da Vinci, o número de oro sencillamente, para nosotros. Se atribuye a Pitágoras el descubrimiento de la razón áurea, del teorema que lleva su nombre y del pentagrama, estrella regular de cinco puntas donde el número de oro es un puntal básico. Hizo de la estrella de cinco puntas el distintivo de los miembros de la escuela filosófica que fundó, el pitagorismo. Los pitagóricos destacaban por su sobriedad, por su altura moral, por su coherencia. El principio fundamental de la filosofía pitagórica era que todas las cosas son números o están formadas por números. Platón, en el Timeo, se hace eco de las enseñanzas pitagóricas. Pues, cuando de tres números, sean lineales, sean planos cualesquiera, el del medio es de tal clase que tiene respecto del último la misma relación que tiene el primero respecto de él; e inversamente, cuando es de tal tipo que tiene respecto del primero la misma relación que el último tiene para con él, siendo entonces a la vez el primero y el último término medio los dos, llega a ocurrir así que todos los términos tienen necesariamente la misma función, que todos desempeñan unos respecto de otros el mismo papel, y en tal caso forman todos una unidad perfecta. Aquí encontramos la definición matemática del número de oro. Lo que Euclides recogerá después en sus Elementos de Geometría como la división en media y extrema razón. Precisamente la estrella de cinco puntas encierra en sus proporciones el número de oro. Es un concepto matemático cuya aplicación en el arte hace producir sensaciones bellas y agradables. Despierta en nosotros una resonancia, ya que el hombre y el universo están gobernados por las mismas leyes. De ahí que los antiguos encerrasen al ser humano perfecto dentro de una estrella de cinco puntas, símbolo de belleza y armonía proporcionada. De que estábamos sujetos a leyes y proporciones semejantes, reflejo del Demiurgo, del Hacedor Divino al ordenar el mundo. Un matemático del siglo XII-XIII, Leonardo de Pisa, más conocido como Fibonacci, descubrió esta sucesión al estudiar la reproducción y muerte de los conejos de su granja. Cada término de la sucesión se genera sumando los dos precedentes. Así, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…Esta sucesión presenta propiedades muy curiosas, entre ellas que el cociente entre dos términos consecutivos se aproxima al número de oro. Aparece en el triángulo de Pascal, en algoritmos de cálculos de máximos y mínimos para funciones complicadas, una de sus aplicaciones está en la óptica física, en el cálculo de trayectorias de rayos luminosos al incidir sobre dos láminas de vidrio planas y en contacto (se aplica a la lectura y grabación de datos digitales a través del rayo láser), etc. Los ejemplos podrían ser innumerables. Si tenemos un rectángulo áureo y le eliminamos el cuadrado del lado menor, el rectángulo resultante sigue teniendo proporción áurea, y así sucesivamente. Esto da nacimiento a una de las espirales más hermosas y recurrentes en la naturaleza; la espiral logarítmica. Esta espiral logarítmica gobierna el crecimiento de muchas formas vegetales y animales; sirva como ejemplo la concha del caracol marino Nautilus, o las caracolas de mar tan presentes en nuestras costas. También en la espiral doble de las flores de girasol aparecen términos consecutivos de la sucesión de Fibonacci, el crecimiento de las piñas de los pinos sigue proporción áurea, un huevo de gallina se puede inscribir en un rectángulo áureo, etc. Y por supuesto, la estrella de mar sigue un esquema pentagonal en su desarrollo. Si tenemos en cuenta que aquí se produce el salto crucial evolutivo desde los vertebrados a los invertebrados comprobamos empíricamente la importancia de nuestra proporción. La simetría pentagonal y la estrella de cinco puntas es la base del desarrollo formal de muchísimas flores y arbustos. Incluso en las proporciones del cuerpo humano aparece el número de oro. La distancia del suelo al ombligo en relación con la altura humana sigue proporción áurea. La proporción áurea gobierna también otras medidas anatómicas del hombre, tal como estudió a mediados del siglo XIX A. Zeising. Como medio y modelo para plasmar la belleza, la divina proporción ha sido usada por todas las culturas, y los pueblos con sentido estético la han aplicado en sus monumentos. Encontramos sus huellas en la gran pirámide, donde la altura del triángulo de sus caras guarda doble relación áurea con la base, en la puerta del Sol de Tiahuanaco aparece el triángulo áureo, en una tumba rupestre en Mira, Turquía, del siglo II a.C. de nuevo sale. No se pierde durante la edad media. El número de oro es la base del arco parabólico y del arco apuntado, innovaciones geométricas que se aplicaron en el gótico. Incluso en numerosas portadas románicas y góticas aparece como borde y frontera el triángulo áurico. En el Renacimiento se recupera de nuevo de una forma masiva en el arte. El hombre de Vitrubio de Leonardo fue concebido para ilustrar el libro del fraile Luca Paccioli, La Divina Proporción. En la Anunciación de la Virgen María también aparece, las dimensiones de La Gioconda son de 89x55 cm., curiosamente dos números consecutivos de la serie de Fibonacci. Precisamente debemos el nombre de sección áurea a Leonardo. En el bellísimo cuadro de El Greco, el Entierro del conde de Orgaz, vemos como el mundo inferior terrestre está gobernado por el rectángulo áureo, y el mundo superior, celeste, está regido por el pentagrama místico y el pentágono en el que se inscribe. A nivel matemático Kepler hace hincapié en la proporción áurea en el marco de sus teorías cosmológicas y cosmogónicas. De nuevo se recupera el número de oro en el siglo XIX, precisamente con la aparición del trabajo de Zeising ya citado sobre las medidas anatómicas en el hombre, y como este autor trabajando sobre miles de mediciones encuentra de nuevo la aparición del número de oro. Así, en la obra de Theodore Cook, The Curves of Life, se aplica la proporción áurea al estudio de las formas botánicas y zoológicas. A principios del siglo XX se inaugura en París una exposición de obras pictóricas bajo el título de La Section d’Or. Su influencia es innegable en las obras de Juan Gris, Picasso y Dalí. Así se puede ver en el cuadro Leda atómica, donde un boceto de Dalí nos indica la estructura del cuadro alrededor del pentagrama. Uno de los principales arquitectos del siglo XX, Le Corbusier, recupera el uso de la proporción en el diseño urbanístico y en la edificación. En 1929 diseña para el Miundaneum, complejo situado en Ginebra que serviría de institución mundial y de sede para la Sociedad de Naciones. El trazado del diseño sigue la proporción de oro. En su obra El Modulor, realizada en 1950, y basada de nuevo en esta proporción, donde trata de sistematizar el diseño de las obras de manera que sean útiles para el movimiento humano. De trabajo llegó a comentar Einstein, es una gama de proporciones que hace lo malo más difícil y lo bueno fácil. Su influencia también se deja notar en la música, en el idioma musical creado por Bela Bartok y basado en el sistema de la sección de oro, que integra movimientos primitivos pentatónicos y afinidades primitivas. Podemos rastrear la influencia de la sección en su obra Concierto para Orquesta, y Cuatro piezas para orquesta. Y anteriormente, Robert Schuman en sus Escenas Infantiles también había usado la proporción de oro para regular el número de compases y los intervalos entre ellos.
